缺失生活经验的数学会怎样?
你有没有遇到过这样的情况,一段话每一个字你都认识,大概也知道说了点什么事情,可是却不明白题目究竟问你的是什么,究竟想让你怎样,而你思来想去不知道该从哪里入手。这个时候,我只想是觉得多读书、多思考、多观察生活,一定会助力你的数学学习、数学解决问题。
一、确定位置,生活与数学。
六年级的复习已经进行到“图形与位置”这部分的内容,讲起“四面八方”,和孩子们聊了聊,这“四面八方”究竟是什么。平面上,前后左右称为四面,东、南、西、北、东南、西南、西北、东北称为八方。一年级的时候除了前后左右还学过上下,上下不在四面是因为上下是立体的、三维空间内的位置了。又谈到了钟楼地下通道的出口,究竟有几个,分别是哪几个。其实这是二年级的内容,还记得自己在十几年前带二年级的时候,设计过一节课,名为《古格探秘》,就利用了Authorware软件的强大交互功能让这部分数学内容走近生活。西大街北口和北大街西口可不是同一个出口,当然,并不是说走错出口你不会到达目的地,只是前进的方向却也着实决定了你的未来。
有学生说老师有导航,我不用担心。导航也有信号覆盖不到的地方,也有遇到重庆或是鼓浪屿这类奇幻地区的可能,也有没电无依无靠的境遇,所以,自己多掌握点东西,并无坏处。我们一直在倡导数学源于生活用于生活,可大多数人依旧把数学定义为“算术”,我想越知道的多,越觉得自己无知,越知道的多,越觉得数学才更伟大。
二、确定岔道,数学与生活。
用一个题目来说明数学的价值,这是一个来自于生活的题目,同样这个题目也明确了数学的价值。这个题目来自于我那个“十万个为什么”的儿子。
题目:某铁路线上有M、A. N三个火车站,M、N两站相距350千米,M、A相距18千米,M站有甲列车,全长550米,正常时速为80千米,A站有乙列车,全长450米,正常时速70千米,由于种种原因,安排甲、乙两车同时各从M、A站发车,都向N行驶,为使甲、乙两车都在正常行驶时,乙车恰好能让过甲车,需在A. N两站间修筑长度相同的火车岔道BFC,BEC,假设发车时,甲、乙两车的尾部分别位于M、A处。
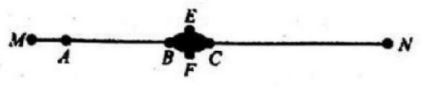
求:(1)火车岔道口B与A站的距离;
(2)火车岔道BEC的长。
问问自己,究竟读懂题目了吗?简单来说,就是一辆车追另一辆车,追及问题。一般地,我会建议先将信息摘录下来,于是我们知道:
MN=350千米,MA=18千米,
甲车(快)追乙车(慢)。
甲车(快)车长550米=0.55千米,
乙车(慢)车长450米=0.45千米
BEC=BFC
问:①AB=?(“火车岔道口B与A站的距离”)
②BEC=?
于是我儿子告诉我,这个题目他第一步肯定没问题,因为路程差÷速度差=追及时间,再用追及时间乘慢车速度就是AB两站间的距离。听起来似乎有些道理,这是追及问题的解题思路。
只是,我问他,你知道什么是铁路岔道吗?他有些迷茫。坐过火车,却未曾有机会观察过铁路,没有机会去认识铁路岔道或者叫做铁路道岔。于是,上网搜索,让他知道铁路岔道的具体样子。再观看视频,明确如何利用铁路岔道实现错车、会车、超车。

再次让他读题,他就清楚了很多。我俩一人拿一个笔盖,做快慢车,根据题目的给定假设“发车时,甲、乙两车的尾部分别位于M、A处”,沿着画好的路线重新走了一趟。我们在操作的过程中,其实有一些小问题,就是我们什么时候可以进岔道而什么时候又该出岔道。后来,我们又一起读了题目,发现了一个词语“恰好”,于是我问他“题目中说恰好,怎样才算恰好呢?”他想了想说,“就是我们离得很近很近但是又撞不上”。我继续问他,“长度呢?你认为长度有什么要求吗?”“只要足够长就好。”
于是,我们再次操作,这次,他全程指挥,当他的车头到达B点时,我的车头紧随着他的车尾,但他似乎并不认可,于是要求我等到他的慢车车尾到达B点时,让我的快车车头也得到达B点。这一瞬间转瞬而逝,之后我们两列车就各行其道了。

继续行驶,在C点,他又提出了要求,让我的车先出岔道,我的快车车尾到达C点时,他的,慢车车头也要同时到达C点。这下真是放心了,因为他说到了同时。

根据题意,结合画图分析:
关于B点,同样的时间里,我们以快车车尾为观察依据,快车所行路程比MB长度少了一个快车车长,从M点行至车头到达B点,而慢车的车尾在B点,也就是说这段时间慢车行了AB,那么快车所用时间就是快车所行路程÷快车速度,慢车所用时间就是慢车所行路程÷慢车速度,因为时间相同,所以我们可以根据这个等量关系列出方程。

解:设AB两站之间相距x千米。
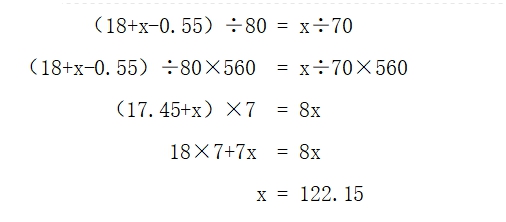
当然,我们也可以直接按照追及问题来思考。
路程差÷速度差=追及时间
路程差:MB-0.55-AB=18+AB-0.55-AB=18-0.55=17.45(千米)
速度差:80-70=10(千米/时)
追及时间:17.45÷10=1.745(时)
AB距离:70×1.745=122.15(千米)
答:AB之间的距离为122.15千米。
同样的方法,我们继续根据图来分析从B点到C点的情况。

首先要清楚,岔道BEC和BFC长度是相同的,慢车行驶的路程比岔道长少一个慢车车长,快车行驶的路程比岔道长多一个快车车长,所以路程差为快慢两车的车长和,速度差仍然为10千米/时,依旧按照追及问题来解决。
路程差÷速度差=追及时间,
路程差:0.55+0.45=1(千米)
速度差:80-70=10(千米/时)
追及时间:1÷10=0.1(时)
岔道长:70×0.1+0.45=7.45(千米)
或80×0.1-0.55=7.45(千米)
当然我们也可以列方程解,设叉道BEC的长为y千米,
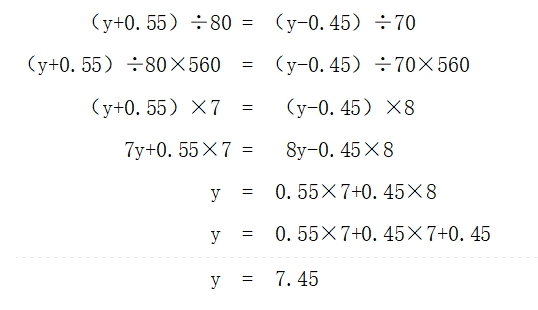
答:岔道BEC的长为7.45千米。
仔细想来,这个题目对于孩子的最大难度在于究竟火车究竟怎么行驶的,而这个生活经验的缺乏导致他无法将题目正确解决。毕竟这个问题的关键就在于究竟两列火车分别走了多少,其实差距只是一列快车长或者一列慢车长,或者是快慢车的长度差也可能是快慢车的长度和。这不由得让我想起了“什锦糖”,我以为我懂得孩子也懂,却不曾想过,他们并不明白究竟什么是“什锦糖”,还以为“什”在这里念“shén”。
数学并不是洪水猛兽,学习数学的价值在哪里呢?细品,真得是处处皆有。 解决完火车岔道这个问题,我还追问了儿子这样一个问题:“你认为题目中的N点有没有价值呢?为什么会说到MN距离为350千米,却又不去用它呢?” 您会觉得该如何去思考这个问题呢?一起思考思考吧。
请遵守《互联网电子公告服务管理规定》及中华人民共和国其他有关法律法规。
用户需对自己在使用本站服务过程中的行为承担法律责任。
本站管理员有权保留或删除评论内容。
评论内容只代表网友个人观点,与本网站立场无关。