思维冲浪

画出来的数学--流程图

翟育敏

一年级学习减法的时候，我们“想加法，算减法”，二年级学习除法的时候，我们根据“乘法口诀”求商，这是我们最早有了加减法互为逆运算、乘除法互为逆运算的认知。在解决一些变式练习如（  ）+3=5，小伙伴们根据对10以内数的加法的熟悉能直接知道填写结果为2，其实将括号换成字母，就是北师大版数学四年级所学知识“方程”了。

对于已知一个数，经过某些运算之后，得到了一个新数，求原来的数是多少的应用问题，它的解法常常是以新数为基础，按运算顺序倒推回去，解出原数，这种方法叫做逆推法或还原法，这种问题就是还原问题。还原问题又叫做逆推运算问题．解这类问题利用加减互为逆运算和乘除互为逆运算的道理，根据题意的叙述顺序由后向前逆推计算．在计算过程中采用相反的运算，逐步逆推。为了便于对这个问题的初步理解，我们常常用“流程图”来帮助解决。

一、关于流程图

1.什么是流程图

流程图是对过程、算法、流程的一种图像表示，通常用一些图框来表示各种类型的操作，用带箭头的线把它们连接起来，以表示执行的先后顺序。用图形表示算法，直观形象，易于理解，有时候也被称之为输入-输出图。

2.数学课本中的流程图

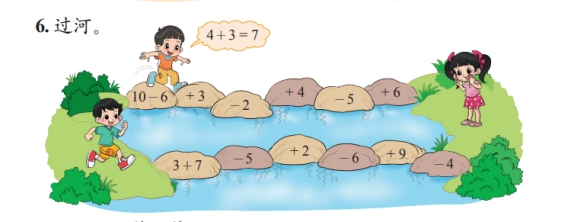
北师大一年级上册中有小朋友过河的图，就是用前一块石头经过运算后的结果，经过下一块石头上的计算指令操作，输出新的结果，进行新的计算。

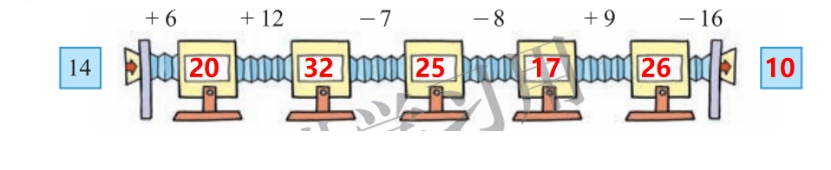
北师大一年级下册中的这幅图更符合流程图的意义，我们输入的数是14，经过了一系列的计算操作后，得到一个结果，这个结果就是输出的数。根据图意，因为有流程中有6步，故我们有以下6个算式：

14+6=20,20+12=32,32-7=25,

25-8=17,17+9=26,26-16=10。

最终输出结果为10。

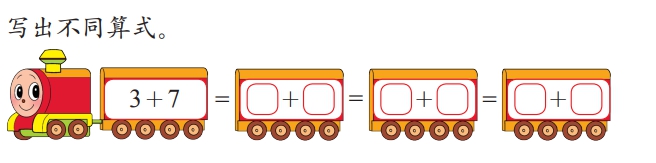
1. 区别与联系

     我们看到过很多火车图，有的是用箭头连接，但也有如下图用等号连接的，这和我们上面所说的流程图并不一样。我们要到达的是每一节车厢得到的结果都是相同的，均为10.

   

   二、计算中的还原问题

 1. 基础问题--开门见山数与计算

某数先加上 3，再乘 3，然后除以 2，最后减去 2，结果是 10，问：原数是多少？

读题的首要问题是要明白，整个题目讲了怎样的事情。依题目而言，我们可以知道原来的数经过一步步计算，得到10，原来的数是未知的，我们可以根据题意得到这样一个流程图：

流程图正着走，我们需要倒着想。第一个想到的就是“谁减2等于10”，我们知道12-2=10，所以最后一个框里填的是12。这个12其实是10+2得来的，因为被减数=减数+差。其实这也是方程初步所有解决的问题。依次为下图：

在解决这个问题时，建议大家使用分步计算，因为步数较多时容易出现运算顺序错误的情况，如，此题就会出现10+2×2÷3-3的情况，这个式子在计算时根据运算顺序，应该是先乘、再除，而后加，最后减，违背了加、乘、除、减的意愿，需要小括号来改变运算顺序后方可正确，即（10+2）×2÷3-3。

2. 思维提升--情境改编计算与还原

一次数学竞赛颁奖会上，小刚问老师：“我得了多少分？”老师说：“你的得分减去 6 后，缩小 2 倍，再加上 10 后，扩大 2 倍，恰好是 100 分”．小刚这次竞赛得了多少分？

遇到这类带有情境的问题，我们“去情境”，把它改编成一个纯计算的题目，它就变得简单许多了。“一个数减去 6 后，除以2，再加上 10 ，最后乘2，恰好是 100 ”。这个问题就变得简单了。

三、单个变量的还原问题

1.不是还原问题的问题--简单与复杂的切换

一只猴吃 63 只桃，第一天吃了一半加半只，以后每天吃前一天剩下的一半再加半只，则多少天后桃子被吃完。

分析题意，首先孩子们会觉得奇怪的是，为什么会吃半只桃子，算下去，就能发现其中的原因，毕竟给的这个63是个奇数，也就是单数，它的一半31.5是个小数，加上半只能凑成整数，也就是说吃的并不是半只。这个问题，只需一步步计算每天吃了多少，每天剩下多少，直到剩下的数量为0。

有学生列了18个算式，解决了这个问题。

我们可以再分析看看，在这个问题中“剩下的数量”一直在出现，我们是否可以只考虑剩下的数量，而不去看吃掉的数量？可以试试看。第一天先吃了63的一半，那么剩下的就是另一半，也就是63÷2=31.5（只），但并未吃足量，所以猴子还得从剩下的这另一半中再吃半个，这时剩下的就是31.5-0.5=31（只）了。也就是说，第一天结束后，桃子剩下了31只。那么我们将原来的“63÷2=31.5
（只），31.5+0.5=32（只），63-32=31（只）”缩减为“63÷2=31.5（只），31.5-0.5=31（只）”，列综合算式为“63÷2-0.5=31（只）”。之后的每一天都是同样的步骤，吃掉一半剩下另一半，再从剩下的另一半里吃掉半个。这样的话，我们可列式解答为：

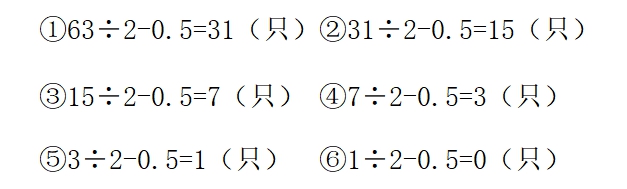
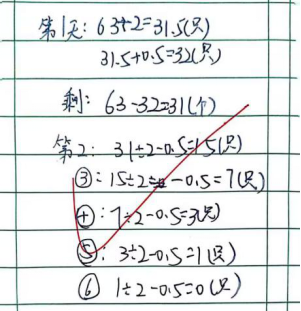
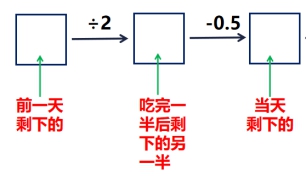
  在解决这个问题时，对于猴子吃桃子这件事情，我们其实已经有了一个明确的流程，即“吃一半就剩另一半后再吃半个”。用流程图表示为：

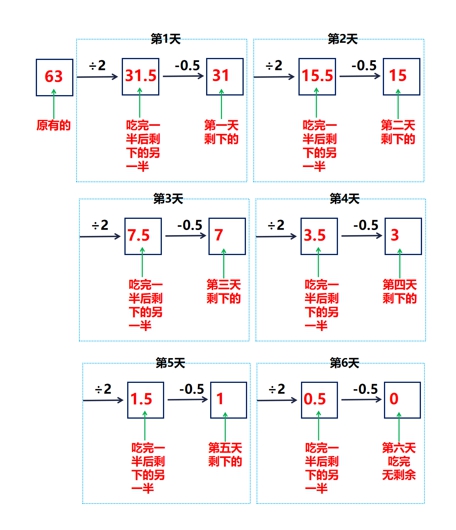
 于是我们根据题意，将流程图补充完整。从流程图能直接看出6天后猴子吃完所有桃子。

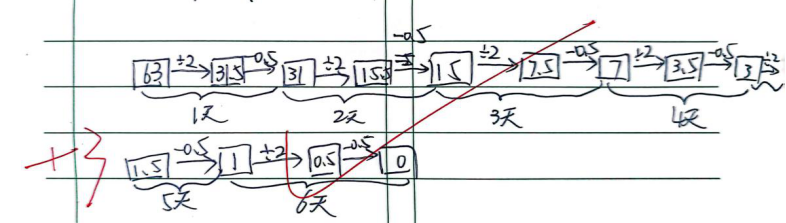
2.流程图解单个量的还原问题--正向与反向的结合

这样的流程图帮助我们理解题意。可确实不是还原问题，所以还是这样一个猴子吃桃子的问题，可以怎么将它变为一个还原问题呢？我们调整一下信息，将这个题目改变为“一只猴吃桃子，第一天吃了一半加半只，以后每天吃前一天剩下的一半再加半只，6天后桃子被吃完。问原来有多少只桃子？”

这成了一个还原问题，根据题意，我们可以绘制一个流程图。那么我们需要关注什么？一定是“剩下的量”，和之前的问题一样，毕竟每一次都是以“前一天剩下的量”为基准“开吃”的。

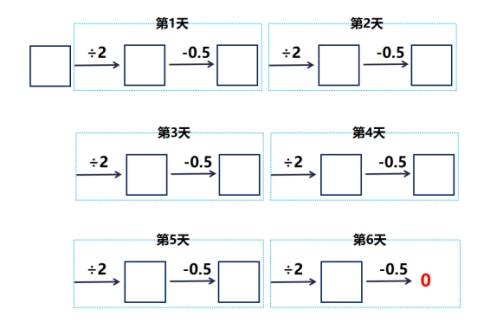
列式为：

四、一题变多题，区分多与少

李奶奶卖一筐鸡蛋，第一位客人买走了一半少 2 个，第二位客人又买走了剩下的一半多 2 个，第三位客人把剩下的 5 个鸡蛋全部买走了。李奶奶的篮子里原来多少个鸡蛋？

此题关键在于“多”与“少”究竟该“加”还是“减”。那么又回到了我们所说的“剩下的”这个关键词了。由题目可知，第一位客人“买走了一半少2个”，我们可以认为，先买走了一半，那么剩下了另一半，这时发现不想买那么多，只想买“一半少2个”，所以就退回来2个，也就是说剩下的就是一半再加上2个。而第二位客人“买走了剩下的一半多2个”，也就是说先买走剩下的一半，然后再买两个，这时剩下的另一半就会再减少2个。这里的多与少就是关键了。

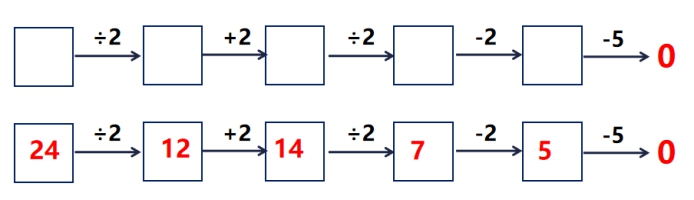
于是我们开始改题，仅仅改动一个或两个字，结果可就大不相同了。

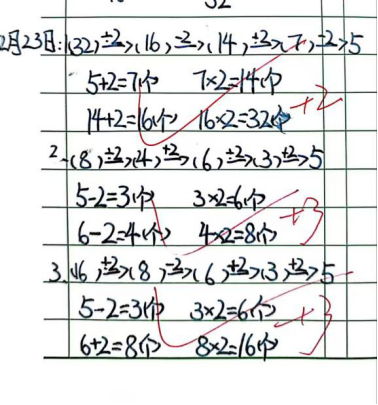
原题：李奶奶卖一筐鸡蛋，第一位客人买走了一半少 2 个，第二位客人又买走了剩下的一半多 2 个，第三位客人把剩下的 5 个鸡蛋全部买走了。李奶奶的篮子里原来多少个鸡蛋？

改1：李奶奶卖一筐鸡蛋，第一位客人买走了一半多 2 个，第二位客人又买走了剩下的一半多 2 个，第三位客人把剩下的 5 个鸡蛋全部买走了。李奶奶的篮子里原来多少个鸡蛋？

改2：李奶奶卖一筐鸡蛋，第一位客人买走了一半少 2 个，第二位客人又买走了剩下的一半少 2 个，第三位客人把剩下的 5 个鸡蛋全部买走了。李奶奶的篮子里原来多少个鸡蛋？

改3：李奶奶卖一筐鸡蛋，第一位客人买走了一半多 2 个，第二位客人又买走了剩下的一半 少2 个，第三位客人把剩下的 5 个鸡蛋全部买走了。李奶奶的篮子里原来多少个鸡蛋？

看看孩子们是如何解决的吧！

画出来的数学，画的是思维，画的是思考，一个流程图解决一类大问题！