螺旋上升的知识及能力
--由“比例”的知识感受每个题目都有它存在的价值
航天城第四小学 翟育敏
于我们年级数学而言,老师和学生手上拥有两本教材,一本北师大版数学,一本人教版数学,两本各具特色。我们上课使用的是北师大版。北师大数学教科书力求从学生经验出发,体现“从头到尾”思考问题的过程,以期达到基础知识、基本技能、基本思想、基本活动经验并重,发现和提出问题的能力、分析和解决问题的能力共同发展。人教版也具有自己鲜明的特色,我们目前把人教作为我们的辅助教学并用。
从整套教科书的内容框架我们可以清楚地看出有些内容在不同学段均有涉及,这是因其所学知识难度不同,所以在不同年级会有不一样的要求。
六年级学习的过程中,学生常常会有疑问,这么简单的问题为什么在六年级出现?
一、比例的基本性质。
例如:人教版教材第44页第15题第(1)问,问到:足球与篮球的单价之比是多少?

这一题在练习八中,而练习八对应的是比例的意义和基本性质。大部分学生在解决这个问题时,毫不犹豫地都选择了单位“1”来解决。所花钱数相等,那么就让这个钱数为单位“1”,那么足球的单价就是钱数的1/6,篮球的单价就是钱数的1/8。所以足球单价与篮球的单价比就是1/6:1/8=8:6=4:3。
也有同学用了设数的方法,他们认为所花钱数一定是6和8的公倍数,所以选择利用6和8的最小公倍数作为所花钱数,即[6,8]=24,设所花钱数为24元,那么足球的单价为24÷6=4元,篮球的单价为24÷8=3元,故足球和篮球的单价比为4:3。
那么问题来了,有同学问:“这个题出到这有什么价值”?有人回答,“为了下一题提供条件”。也有人说“这个问题放到这里确实没什么实际作用,就是把学过的东西拿出来用了一下”。我没有直接回答,只是问了问大家,除了上述这两种方法,你还有别的方法吗?只有万同学一人表示自己的做法和大家不同。她向大家展示了自己的方法,她认为:
我们的目标是求足球单价与篮球单价的比是多少,其实就是想知道足球单价:篮球单价=( ):( )。
根据题意可以得到一个关系式,足球单价×6=篮球单价×8,那么根据这样一个乘法等式,联系刚学的知识点,这其实就是一个积相等的式子。
因为“在比例里内项之积等于外项之积”,根据一个积相等的乘法等式,我们一般能写出八个比例。在“足球单价:篮球单价=( ):( )”中,足球单价是外项,另一个外项就应该是8,篮球单价是内项,另一个内项就有应该是6。那么就有“足球单价:篮球单价=(6 ):( 8 )”,也就是“足球单价:篮球单价=(6 ):( 8 )=3:4”这样的结论了。
恍然大悟的小伙伴们,这才明白这个题目出现在这里的深意了。不是为了别的题目,而是比例的基本性质自身本就有重要的价值。
螺旋上升的知识,看似在解决原有的问题,却已经变成了新的问题,知识水平在提高,学生的能力也在提升。
二、反比例的应用。
又如:最近我又出了这样一个问题“一架飞机的燃料能用9小时。出去时每小时飞1500km,回来时每小时1200km,问这架飞机最多能飞多少千米就要返回?”
为什么说“又”呢?因为这个题目学生在四年级见过,在五年级见过,这次出现在六年级。为什么同样的题目会出现在不同的年级呢?难道知识为了“熟能生巧”或者只是传说中的“刷题”?当然不是。
第一次出现在四年级,是学生学习了“方程”这一单元。抓住问题核心也就是往返路程相等这一等量关系,不确定的就只剩下时间了。但去的时候和返回的时间之间也有关系,往返总时间为9小时。所以,我们拥有两个等量关系,即“去的时间+回来时间=9小时”和“去的路程=回来路程”。我们可以用一个等量关系设未知数,另一个等量关系列方程。
根据第一个等量关系“去的时间+回来时间=9小时”设未知数。
解:设去时用了x小时,那么回来用了9-x小时。
根据第二个等量关系“去的路程=回来路程”列方程。
1500x=1200×(9-x)
1500x=10800-1200x
2700x=10800
x=4
因为路程=速度×时间,与去时速度1500对应的时间是4时,那么路程为1500×4=6000(千米),也就是最远行至6000千米。
我们是否可以用“去的路程=回来路程”设未知数,而用“去的时间+回来时间=9小时”列方程呢?
当然可以,但问题就会接踵而至,这样的方程四年级的孩子能够列出来,但如何解方程成了问题。
所以,这个问题在五年级学习了分数乘除法后就能得到解决。此时只需根据问什么设什么的原则,设最远路程为x千米,就能实现对问题的解决。
解:设最多飞行x千米就要返回。
根据第二个等量关系“去的时间+回来时间=9小时”列方程。
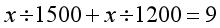
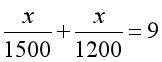
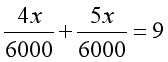
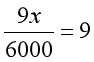
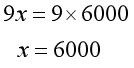
五年级和四年级的区别就在于因为计算能力的提升,让解决这个题目方法的可行性变多了,那么六年级再做还有价值吗?
这个题目放置的位置在六年级第四单元《正比例与反比例》第4课时《反比例》学习后。也就是在这个时候,学生问我“为什么会做的题目还要再做一次”,我回问学生,你“觉得是为什么呢?”我还问“为什么我要在这一个单元提出这个问题?”学生思考后并未得到答案。于是我们进行与本单元内容相关的知识探究,往返路程相等,也就是路程一定,当我说出“那么路程一定时”,学生很快回答“速度和时间成反比例”。因为这是最近正在学习的内容,学生回答得很流利。所以,突破点就出现了。路程不变时,速度和时间成反比例,速度越快所用时间就越短。已知往返速度比是1500:1200,也就是5:4,那么所用时间比就是4:5,下来我们需要做的就是将9个小时按照4:5来分配,那么当速度为1500千米/时的时候,时间就是4个小时,所以路程为1500×4=6000(千米)。
同一个题目在不同的年级有着不一样的方法,螺旋上升的不仅仅是知识,更有学生对题目的理解能力,对数学之间联系的分析能力。当真正弄懂了题目出现的目的,也就读懂了教材的意图,读懂了数学之间的知识联系。这样的螺旋进阶思考是我们想要的提升。
请遵守《互联网电子公告服务管理规定》及中华人民共和国其他有关法律法规。
用户需对自己在使用本站服务过程中的行为承担法律责任。
本站管理员有权保留或删除评论内容。
评论内容只代表网友个人观点,与本网站立场无关。