首页 >> 校园动态 >> 学科主页 >> 数学 >> 思维提升营 >> 思维冲浪 >> 正文

教材的“放”，老师的“收”

2022年05月12日 11:53 翟育敏打印　[字号：大中小]

教材的“放”，老师的“收”

--一个例题引发的思考

航天城第四小学翟育敏

数学北师大教材编写以“情境图+问题串”的形式，给老师们非常大的空间。教材越开放，我们老师发挥的空间越大，在教学中，我们如何与教材形成收放自如，今天就以北师大一个小内容作为切入点，进行探索研究。

北师大六年级上册第一单元《圆的周长》一课，试一试有这样的内容：

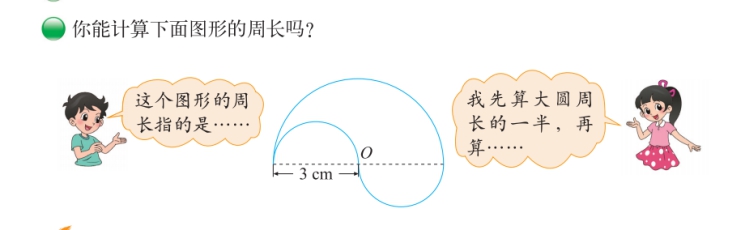
就这样一个材料，你会如何处理呢？

普通处理：

解决此问题，如图中的小女孩一样，先计算出大圆周长的一半，再计算两个半圆弧组成的小圆的周长，两者相加就是这个图形的周长。

即：

小圆周长：3×3.14=9.42（厘米）

大圆周长的一半：3×2×3.14÷2=9.42（厘米）

如果熟练，可以直接用π与r相乘，也就是3×3.14=9.42（厘米）

再算两部分的和：9.42+9.42=18.84（厘米）

作答，图形的周长为18.84厘米。

进阶处理：

1.改题：如图所示，小猫和小狗都要从点A到点B，小猫沿着黑色圆弧走，小狗沿着红色小圆弧走，已知小猫和小狗的速度相同，谁先到达点B？

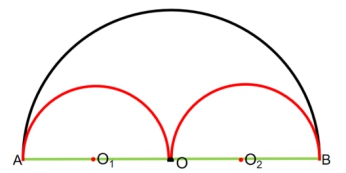
解析：速度相同，路近的先到，路远的后到。所以，需要知道黑色和红色两条路哪条更近一些。小猫走的是大圆周长的一半，小狗走的是一个小圆的周长。因此，只需比较这两者就好

半径不知道，所以可以采用设数的方法。比如，小半圆的半径为1，直径为2，那么小圆的周长就是2π；大圆的半径是2，直径是4，周长是4π，大圆周长的一半就是2π。两种路线长度相同。这里保留π是为了方便计算。

2.再改：那如果图形再次改变呢？

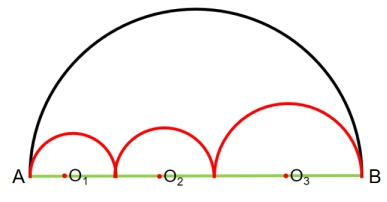
分析：这种情况，我们并不能确定三个小半圆的半径或直径，那么如何解决呢？我们依然可是设数，只是这时的设数并不能代表所有情况，所以，我们需要选择用字母来表示。如，我们可以d₁、d₂、d₃分别代表三个小半圆的直径，那么大半圆的直径是这三个小半圆直径之和。

半圆O₁弧长为圆O₁周长的一半，即1/2πd₁，

半圆O₂弧长为圆O₂周长的一半，即1/2πd₂，

半圆O₃弧长为圆O₃周长的一半，即1/2πd₃，

这三个半圆弧长的和为1/2πd₁+1/2πd₂+1/2πd_3，合并同类项为1/2π（d₁+d₂+d₃）。

大半圆弧长为大圆周长的一半，大圆半径为d₁+d₂+d₃，则周长一半为1/2π（d₁+d₂+d₃）。

因为1/2πd₁+1/2πd₂+1/2πd=1/2π（d₁+d₂+d₃），所以小猫和小狗走的路程一样，同时到达。

结束了吗？并没有。在这一单元学习完圆面积计算公式后，回头望一下，将之前设计过的图案、求过周长的图形均拿出来，看看有什么发现。

高阶处理：

1、回头看--它俩面积一样吗？

我们曾经研究过的内容，大家还记得长度相等，那么面积呢？长度相等，大半圆面积与两个小半圆面积一样大吗？

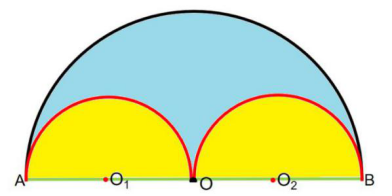
生1：面积也相等。

生2：明显不相等。大半圆面积大于两个小半圆面积和。

师：大半圆半径是小圆半径的两倍，我们知道半径是2倍关系时，面积是4倍关系，那么是不是说大半圆面积是小圆面积的4倍呢？

生3：看着不像啊。

师：那你看着像几倍关系？

生3：2倍。

师：那么想办法验证下你的猜测是否合理？

生3：我可以设数，设小半圆半径为1，那么大半圆半径就是2。两个小半圆组成了一个小圆，小圆面积为1²π也就是π。大半圆面积为2²π÷2＝2π。2π是π的2倍，所以大半圆面积是小圆面积的2倍。那么蓝色部分和黄色部分面积一样大。

师：谁能帮我解释一下为什么是大半圆面积与小圆面积是2倍关系而不是4倍关系呢？

生4：因为这里的小圆是整圆而不是半圆，如果是一个大半圆面积与一个小半圆面积，那么就是4倍关系了，而这里说的是大圆面积的一半与整个小圆面积，所以只是2倍关系。

2、大胆想--大小半圆啥关系？

师：那么我是否可以归纳规律：当大半圆直径等于小半圆直径之和时，大半圆的弧长等于几个小半圆弧长的和，大半圆面积是几个小半圆面积和的2倍呢？

生4：可以。弧长上次已经用字母验证过了，这次的面积也用设数法验证了，所以，可以如此总结。

生5：看起来好像是可以，那么咱们再换一种试试看。

师：比如，这样的图形。大半圆面积是否等于三个小半圆面积和的2倍呢？

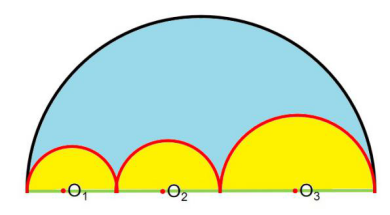
大半圆的直径等于三个大小不同的小半圆的直径和，大半圆的半径等于三个大小不同的小半圆的半径和。如果我们令三个小半圆的半径分别为r₁、r₂、r₃，那么三个小半圆的面积分别为1/2πr₁²、1/2πr₂²、1/2πr₃²，面积和为1/2π（r₁²+r₂²+r₃²）。大半圆的半径为r₁+r₂+r₃，大半圆的面积为1/2π（r₁+r₂+r₃）²。