简单却复杂，复杂亦简单
西安航天城第四小学 翟育敏
“简单却复杂，复杂亦简单”，这是一句辩证的话语，它源自于唐彩斌老师在与孩子们共同研究《三角形面积》时的一番话。数学中的简单承载着复杂，而复杂也可能带来简单。究竟是简单好还是复杂好呢？我们也得辩证地看。
让我们用一个例题来体会下简单与复杂。
例：有甲乙两块含铜率不等的合金，甲块重12千克，乙块重18千克。现从两块合金上各切下重量相等的一部分，将甲块上切下的部分与乙块剩余的部分一起熔炼，再将乙块上切下的部分与甲块上剩余的部分一起熔炼，得到的两块新合金的含铜率相等，从每块切下的部分各重多少千克？
读完这个题目，你有什么想法？其实从作业不难看出，班里有想法的孩子，这个题基本都空着，标上了“☆”，这是留给我的内容，于是我们共同研究解决。
我们从读题开始，一边读题一边记录下主要信息：
甲，12千克，含铜率？
乙，18千克，含铜率？
关键句，也就是等量关系“得到的两块新合金的含铜率相等”
写成等量关系式： 新得到的甲块含铜率=新得到的乙块含铜率
交换的过程，交换的是相同质量，但内容不确定，因为含铜率不确定。
所以，我们会发现，在这个题目中我们未知的太多，不知道甲原来的含铜率，不知道乙原来的含铜率，也不知道究竟交换了多少千克，索性我们把这些未知的都用字母来表示。
方法一：设三个未知数--简单的关系，复杂的计算。
解：设甲块原来的含铜率为a%，乙块原来的含铜率为b%，从每块上切下来的部分重x千克。
据题目，我们已知等量关系式：甲现在的含铜率=乙现在的含铜率
即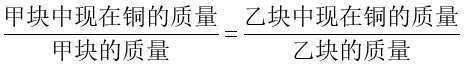 
甲块现在是混合而成，其质量未发生改变，仍为12千克。只是铜的含量发生了改变。这时的铜包括两部分，一部分是含铜率为a%的自身剩下的，也就是（12-x）千克的a%，另一部分是含铜率为b%的来自乙块的铜，也就是b%x。
同样的，乙块现在的铜也包括两部分，一部分是含铜率为a%的来自甲块的x千克，也就是x千克的a%，另一部分是含铜率为b%的自身剩下的铜，也就是b%（18-x）。
因此，我们可以列出这样一个方程：
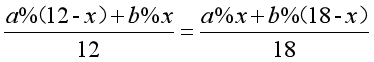
其实这个方程难就难在解方程，但只要仔细去尝试，一步步来，就不会出现太多问题。
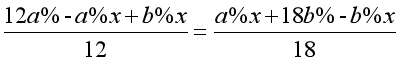
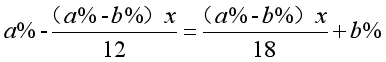
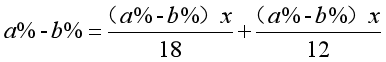
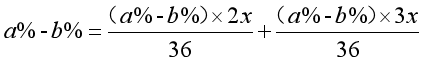
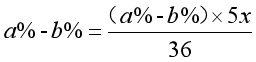
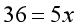
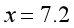
答：从每块切下的部分各重7.2千克。
在解方程的过程中我们发现，虽然我们的方程中有三个未知数，但是在解方程的过程中我们有两个未知数在不知不觉中就那样抵消掉了，这也就是我们常说的“设而不求”。
方法二：设数、设未知数--大胆的猜想，小心的求证。
我有一个问题想问问大家：“甲乙两块的含铜率大小是否会对切下部分的质量产生影响？”大家可以尽可能的猜测。
其实基于我们对这个题目内容的了解，基于我们列方程解决此问题的过程，我们不难发现甲乙两块的含铜率大小不会对切下部分的质量产生影响。取巧一点想就是如果有影响那就没办法解决问题了。结合方程，我们会发现在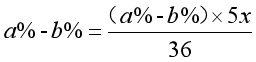这一步中，我们给方程左右两边同时除以
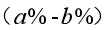，等式仍然成立，也恰好在这一步，我们设的三个未知数只留存下来了问题中的x千克，也就是说无论含铜率到底是多少，最终都会抵消掉，所以含铜率的多少并不会影响切下部分的质量。
既然如此，我们可以任意设定一个含铜率，比如，我们可以设甲块原来的含铜率为10%，乙块原来的含铜率为20%，那么当内部交换后，得到的相等的含铜率就是（10%×12+20%×18）÷（12+18）=16%。我们现在未知的量只有切下的铜的质量x千克，依然根据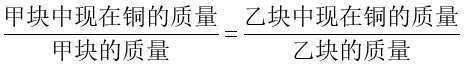这样的等量关系式列方程：
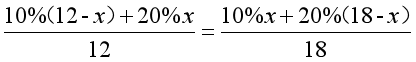
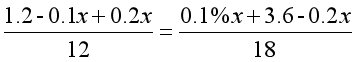
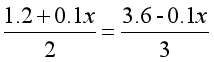
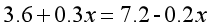
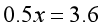
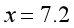
这样的方程在计算上比含有三个未知数的方程还是简单了许多。
方法三：极值--复杂的思维基础，简单的解题过程。
10%、20%既然可以，那么如果再来点特殊的或者是极端的数据呢？是否也依然成立的，那我们可以考虑尝试下极值。
往极端想，假如甲块是100%的纯铜，而乙块是不含铜的金属，也就是0%的含铜率。联想我们的糖水，甲全是糖，乙全是水，那么当我们把这12千克的糖和18千克的水完全混合在一起之后，得到的糖水的含糖率为12÷（12+18）=40%。那么这时，甲杯中的糖就有12×40%=4.8（千克），而原来有12千克的糖，所以给乙的那部分就该是12-4.8=7.2千克。同样的，说回100%的铜与含铜率0%的金属，道理是同样的。所以如果我们采用极值的思想，那么只需简单的过程就可以解决问题。
方法四：构建比的关系，发挥比的作用、
记得杨红艳老师的《生活中的比》一课中曾问学生一个问题，“既然我们已经学习了除法和分数，为什么还要学习比”？经过讨论，学生们找到了学习比的价值，而其中一个内容就是比就像一个模子，背后藏着很多符合这个标准的量。而例题中的问题，我们也可以用比的知识来解决。甲块与乙块的质量比为12比18，也就是2比3，由于要进行等质量的交换，交换后正好含铜率相同，那么我们只要保证我们分割或者合成的每一块内含有甲乙的质量比均为2比3，就能得到一块块含铜率相等的合金。所以，新合成的合金中，第一块只需保证包含的原来甲乙两类的质量比为2比3，也就是包含甲12÷（2+3）×2=4.8（千克）即可，那么剩下的部分就应该来自原来乙块，同样的甲块剩下的部分也转移给了乙，也就是12-4.8=7.2（千克）。
这个问题，我们在解决时往往用的是最后极值的方法，只是我们在用此方法时秉承着弄懂算理的原则，问问孩子们“为什么可以用极值思想”。所以，若从看似复杂的方程入手，一点点让学生明白显得很重要。而我们曾经解决过的很多问题，和它的道理一样，可以设值，可以考虑特殊情况，甚至可以考虑极端情况，例如长方形内的动点P的移动，不会改变影响阴影部分的面积。
“简单却复杂，复杂亦简单”，同学们，一探究竟，方知简单与复杂之间的关联。
陕公网安备61019402000107号
请遵守《互联网电子公告服务管理规定》及中华人民共和国其他有关法律法规。
用户需对自己在使用本站服务过程中的行为承担法律责任。
本站管理员有权保留或删除评论内容。
评论内容只代表网友个人观点,与本网站立场无关。